[最も欲しかった] 点対称の図形の書き方 158462-点対称な図形の書き方

図形の対称移動の作図手順と性質 数学fun

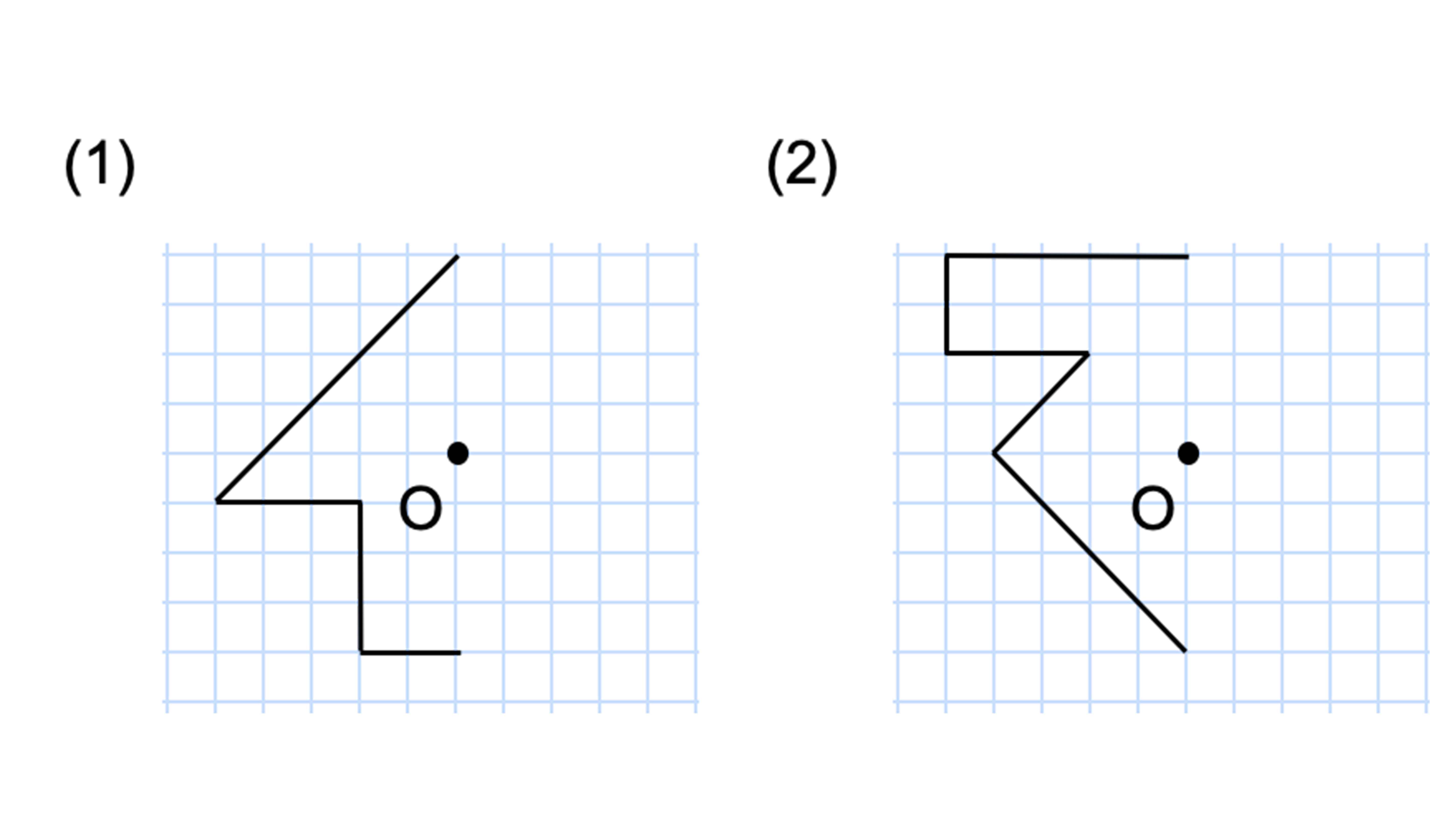
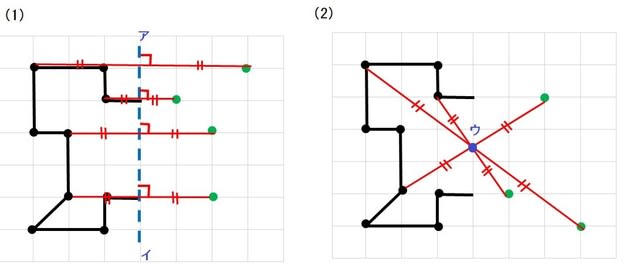
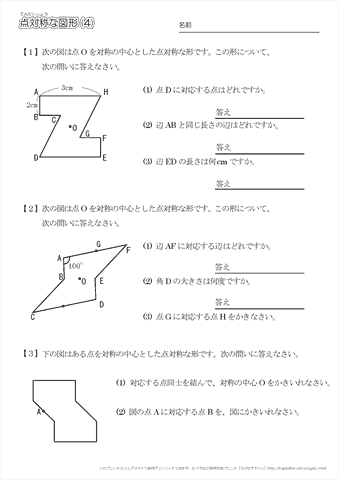
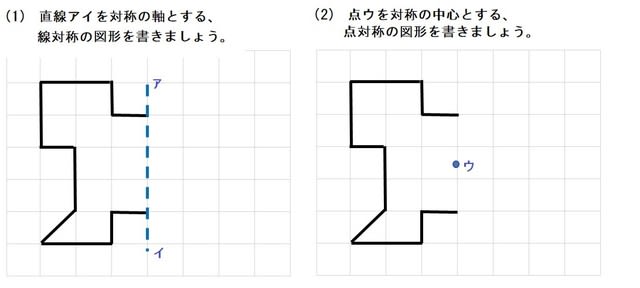
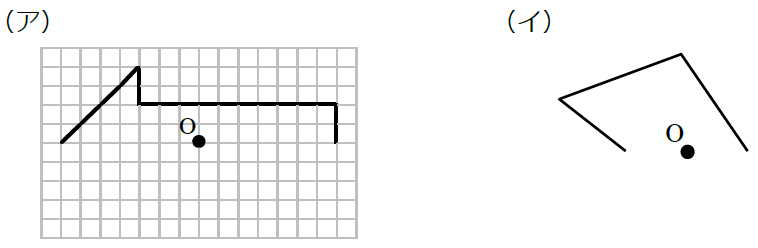
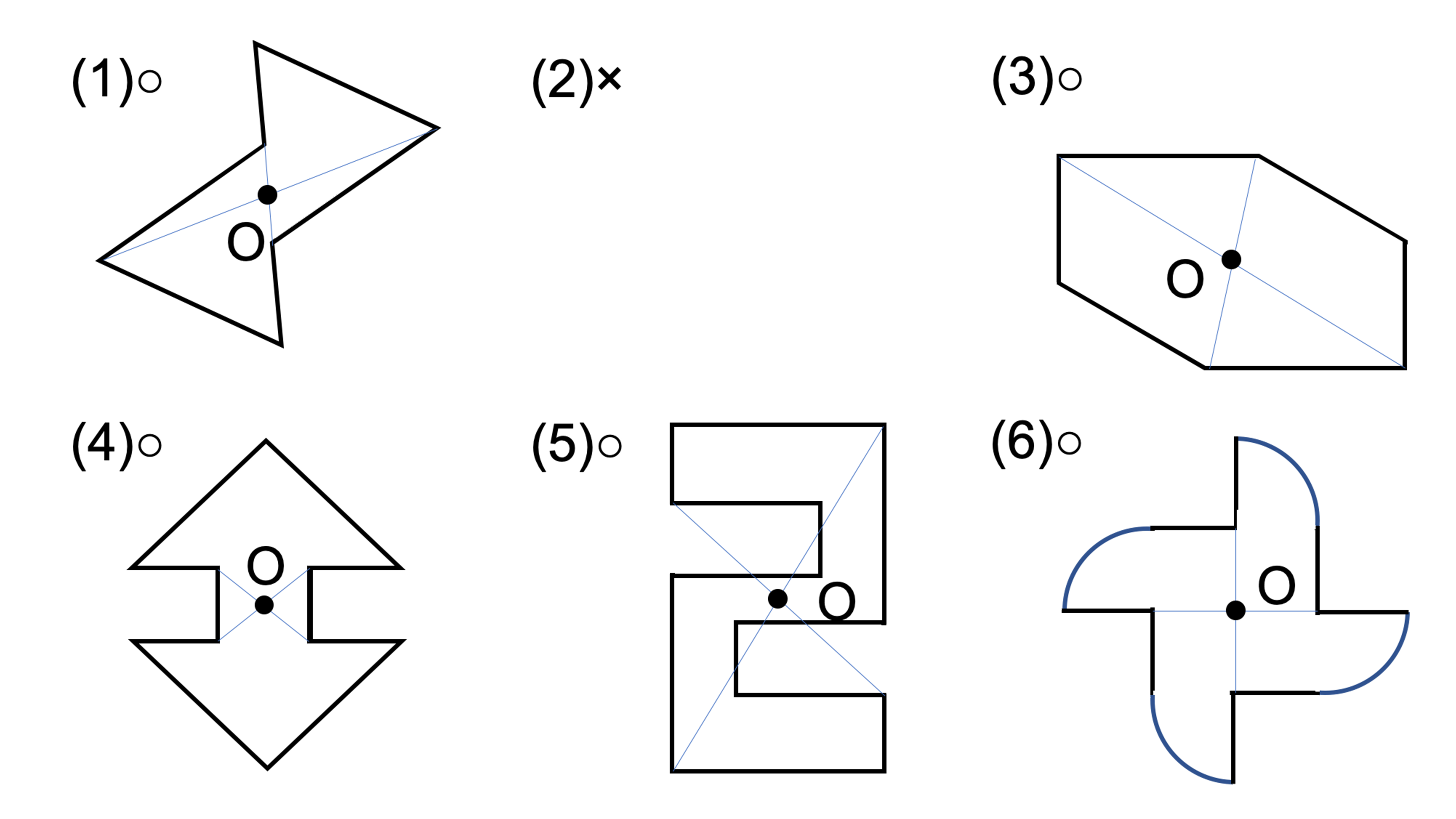
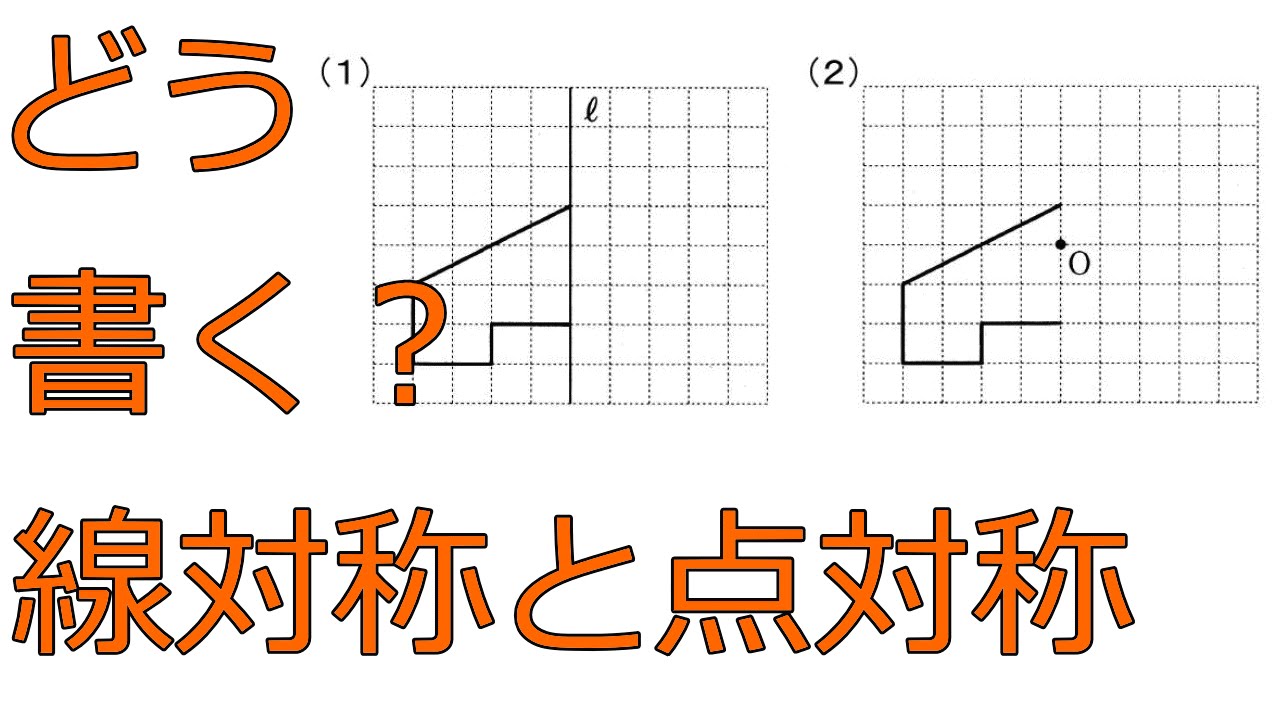
次の記号はいずれも線対称な図形である． 各々赤で示した直線を対称軸として折り返すと元の図形と重なるから，これらは線対称な図形であるが， 左の2個は対称軸が2つあるのに対して，右の2つは対称軸は1つである 点対称な図形 解説 次の図のように休業中の課題についての補足説明 算数（対称な図形） 〇線対称のかき方 ① ②それぞれの点を通り， 直線アイに垂直な線を引く。 （簡単に等しい点をとる方法を考えてみよ う！） ③ 点を結ぶ。 〇点対称の書き方。 直線アイまでの長さと等しい点をとる。

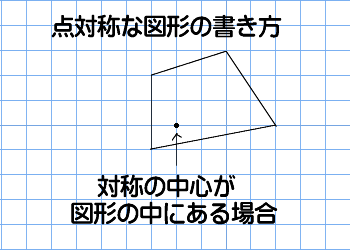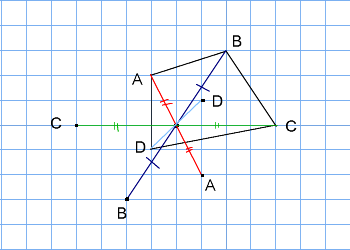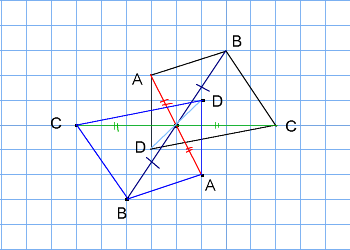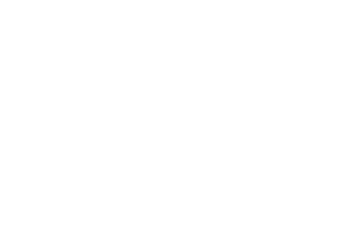
点対称な図形の書き方

点対称な図形の書き方- 点対称とは 2 今回は点対称な図形の書き方です。 点対称な図形を書けという問題では、方眼ありの時となしの時があると思います。ありの時はもう既に書いてある片方を逆さまにしてくっ付ければいいだけです。 なしの時がめんどいんですよ6年算数線対称点対称図形 わかる教え方 🎇 上の図にならって性質を書き変えると下のようになります。 よく間違えるところですから、お子さんが正しく理解できているか注意して見てあげてください。 16 そのとき、結んだ線が全て1点で交われば、点

線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード

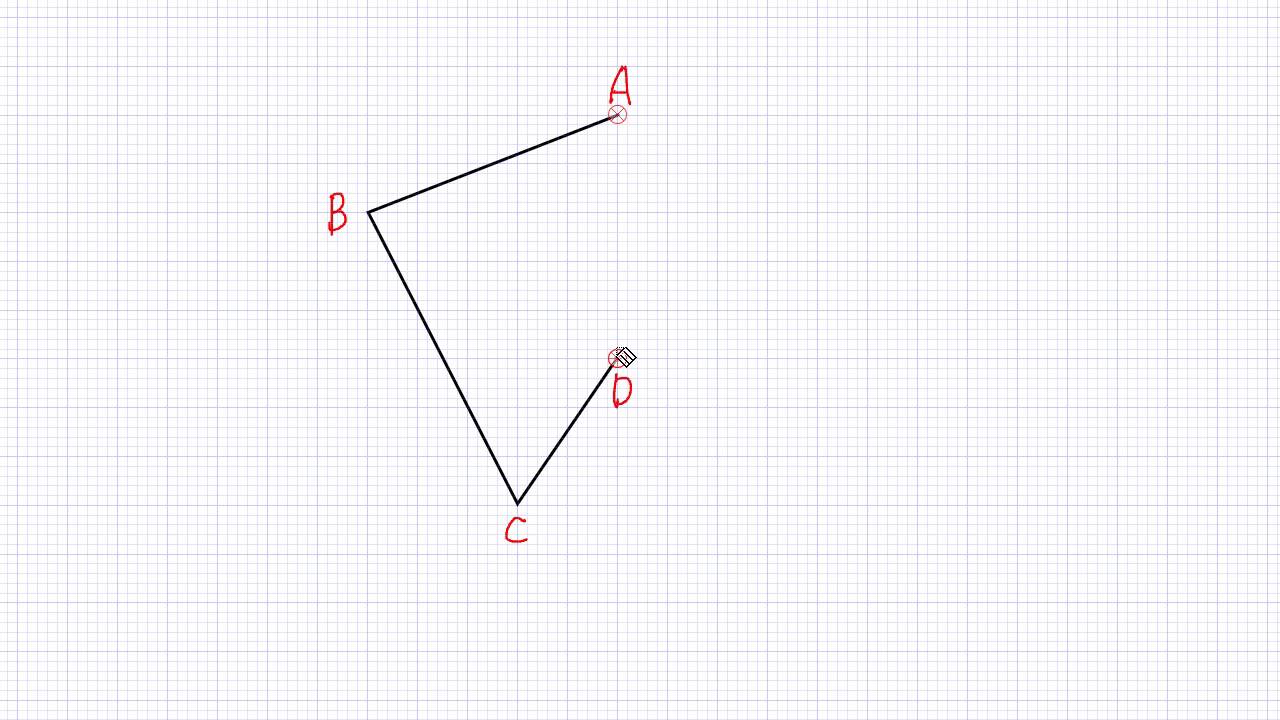
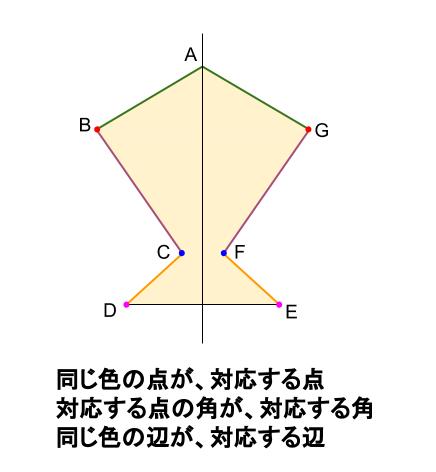
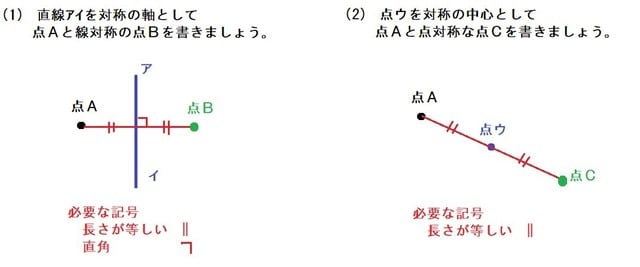
アドインの使い方 (Ver8 の場合) アドインの使い方 (Ver7 の場合) アドインの使い方 (Ver6 以前の場合) 「中心線」の実行方法 メニューの アドイン から 中心線 を選択します。 中心線の対象の図形 図形1、 図形2を選択します。 中心線を作図する開始点今日の講義内容 日本工業大学製図の基礎 (1)正面図の選び方 (2)必要な図面の選び方 (3)第三角法の復習 (4)線の種類の復習点対称な図形を作るための条件！ ①対応する点を結ぶ直線は対称の中心 を通る。 ②対称の中心から対応する点までの長さ は等しくなっている。 つまり，この画像では点Aからの直線は 対称の中心を通っているので，点Oから

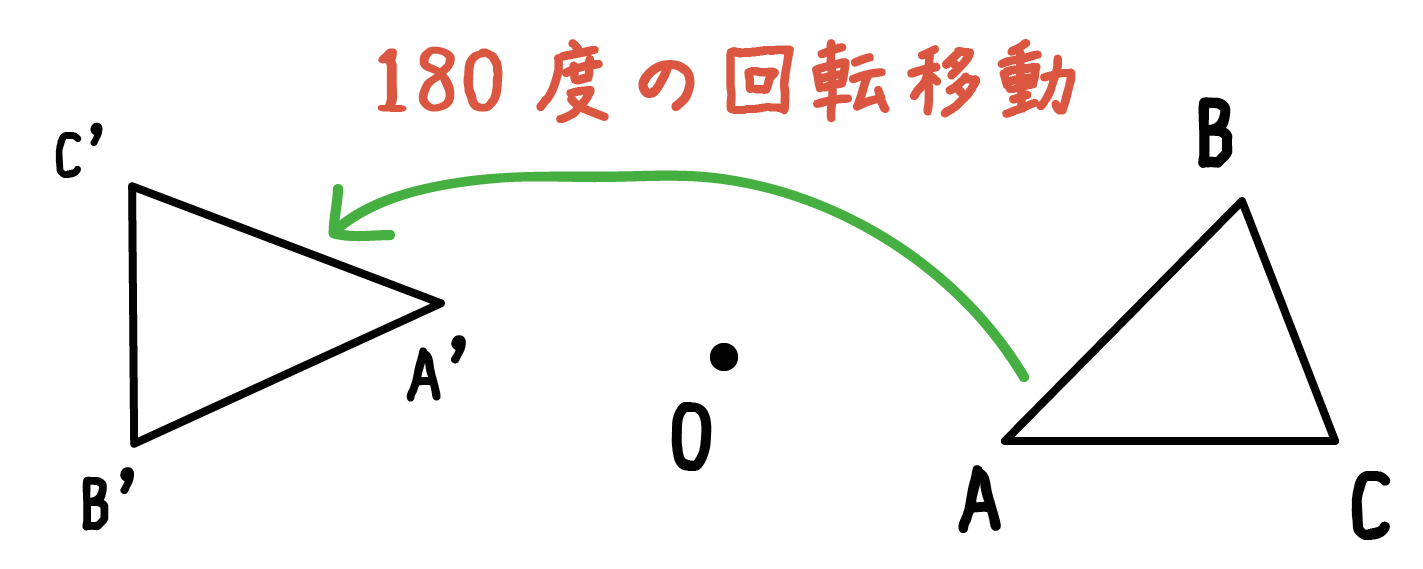
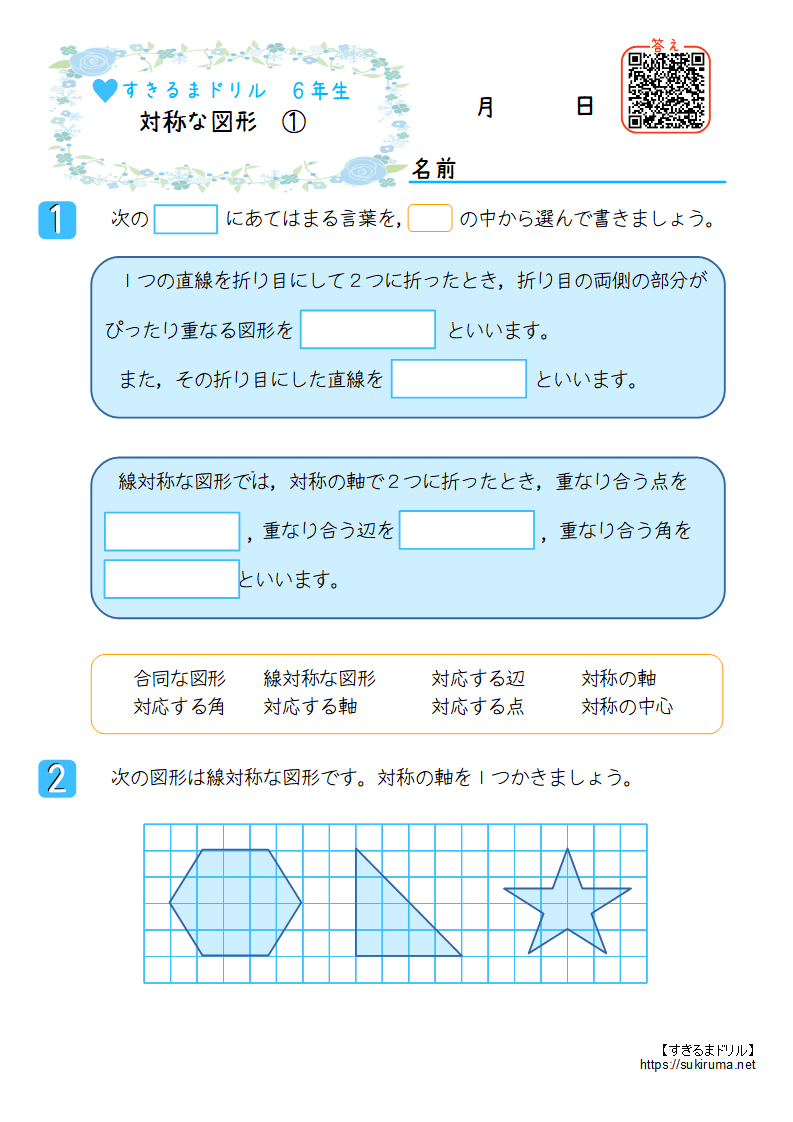
小学6年生の算数 線対称な図形 問題プリント 無料ダウンロード・印刷できる、線対称な図形の練習問題プリント です。 線対称な図形の意味と性質、図形さがし、作画などを練習し、理解を確かめることのできるプリントです。回転移動とは、ある点を中心として図形をある角度だけ回転させる移動のこと。 このとき、中心とした点のことを回転の中心といいます。 また、180°の回転移動を点対称移動というので覚えておきましょう！ 回転移動の作図はちょっと難しい 悩みのタネは、「線対称」と「点対称」に由来している、と思う。 それぞれ、私の教育課程では中学初期に現れた。 「線対称」・・・ ある線を基準に図形を分けたとき、双方の図形が一致する性質。 鏡像対称ともいう。 「点対称」・・・ ある点を

点対称な図形の書き方のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン	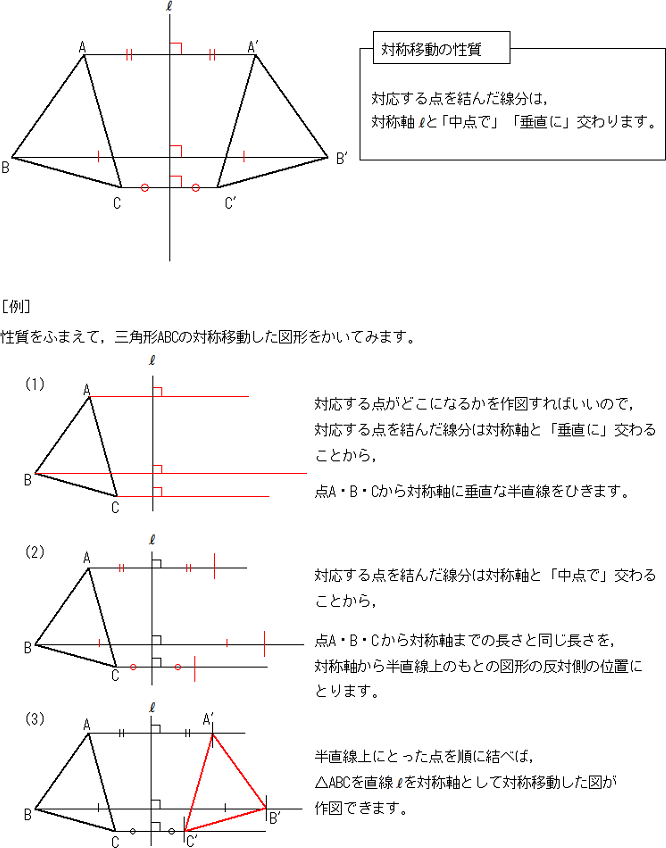中１数学 点対称な図形とは まなビタミン
中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン
中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン	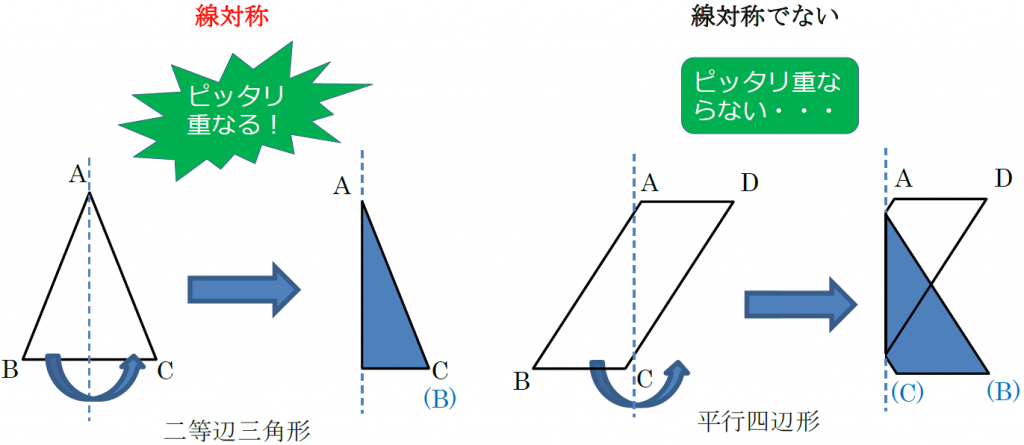中１数学 点対称な図形とは まなビタミン
中１数学 点対称な図形とは まなビタミン	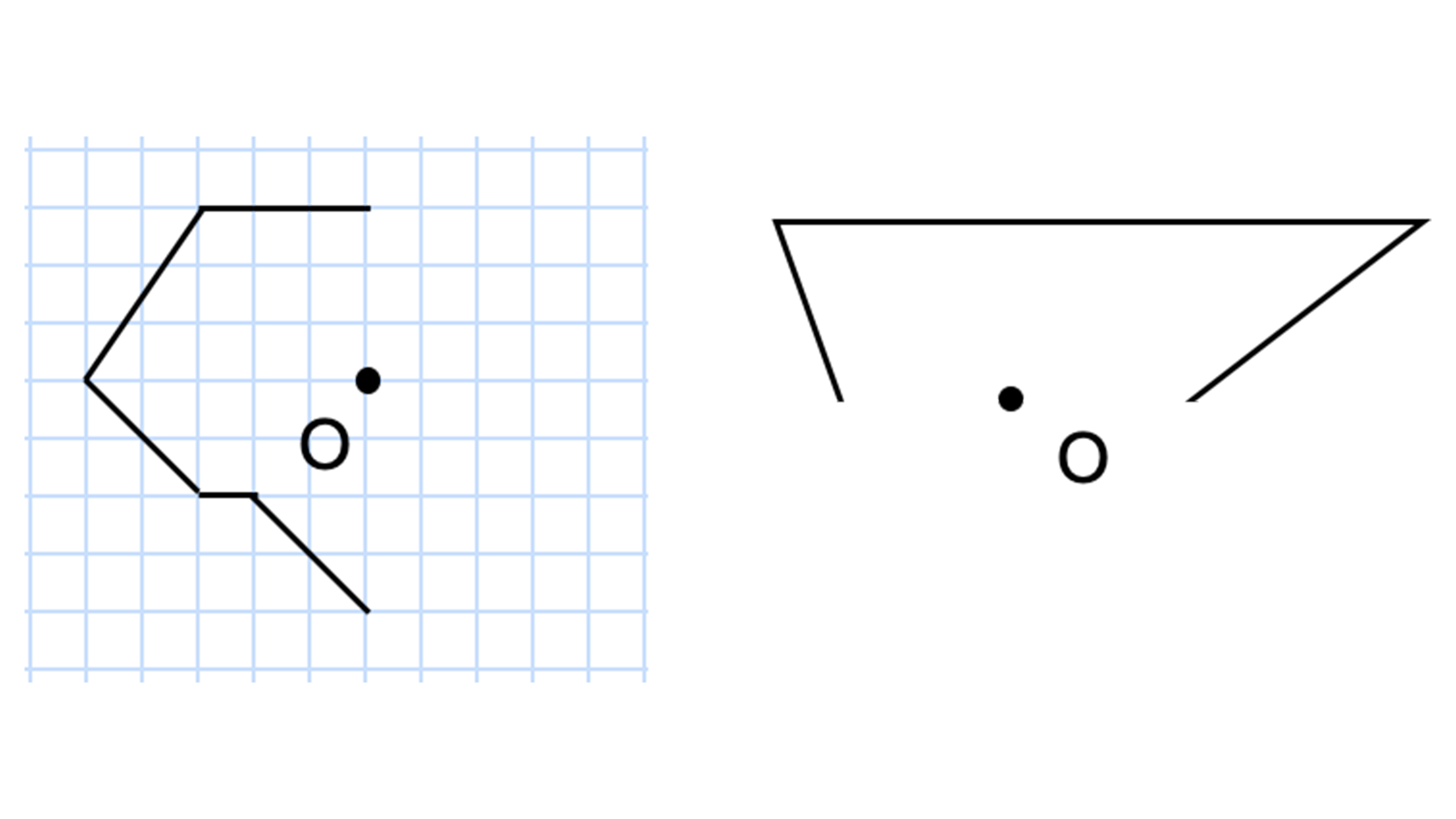中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン
中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン
中１数学 点対称な図形とは まなビタミン	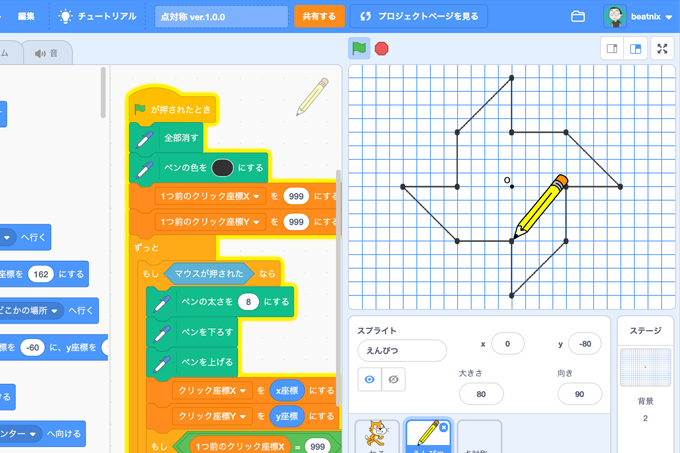中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン
中１数学 点対称な図形とは まなビタミン	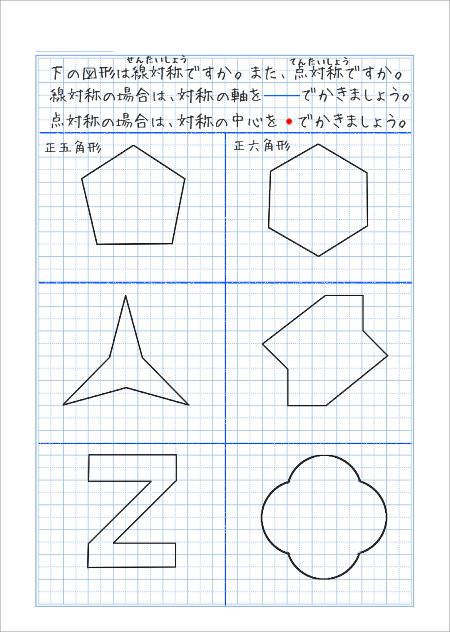中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン
中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン
中１数学 点対称な図形とは まなビタミン	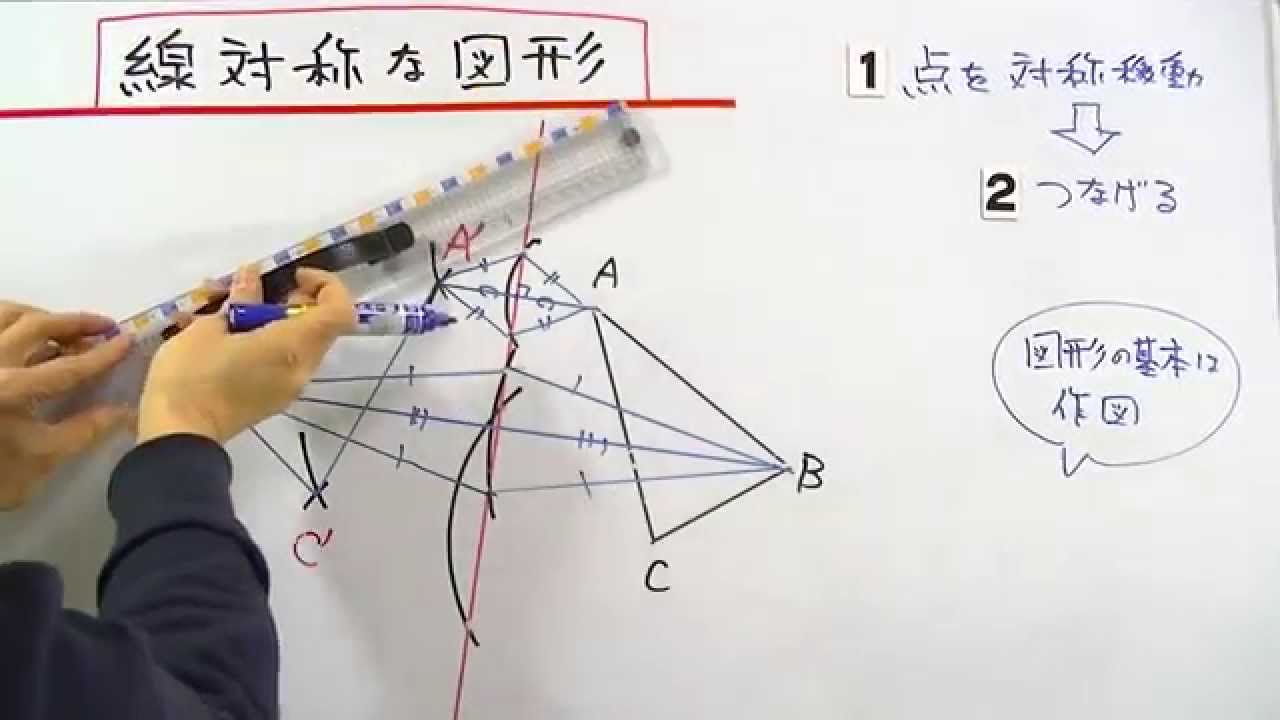中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン
中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン
中１数学 点対称な図形とは まなビタミン	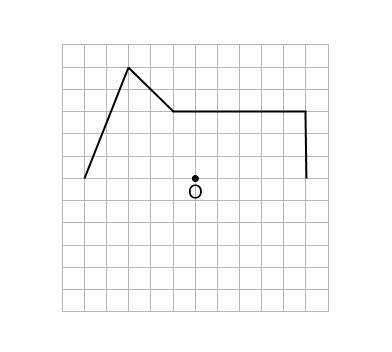中１数学 点対称な図形とは まなビタミン	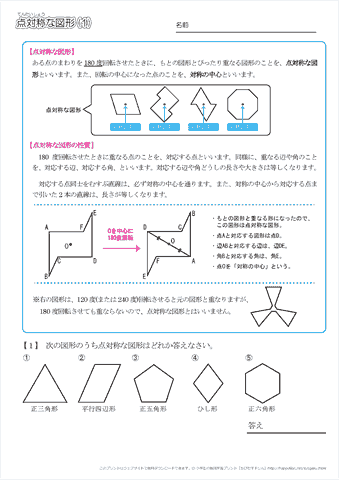中１数学 点対称な図形とは まなビタミン
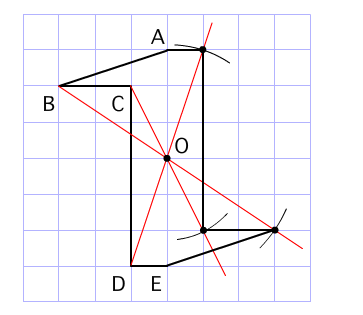中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン
中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン
中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン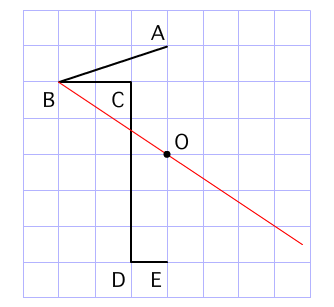
中１数学 点対称な図形とは まなビタミン	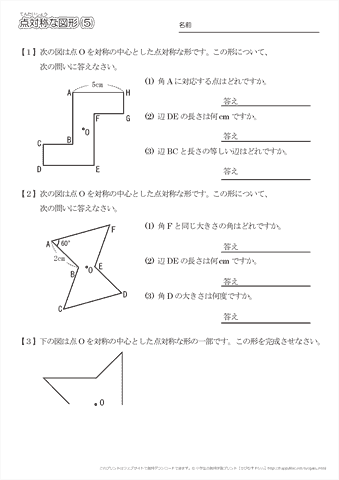中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン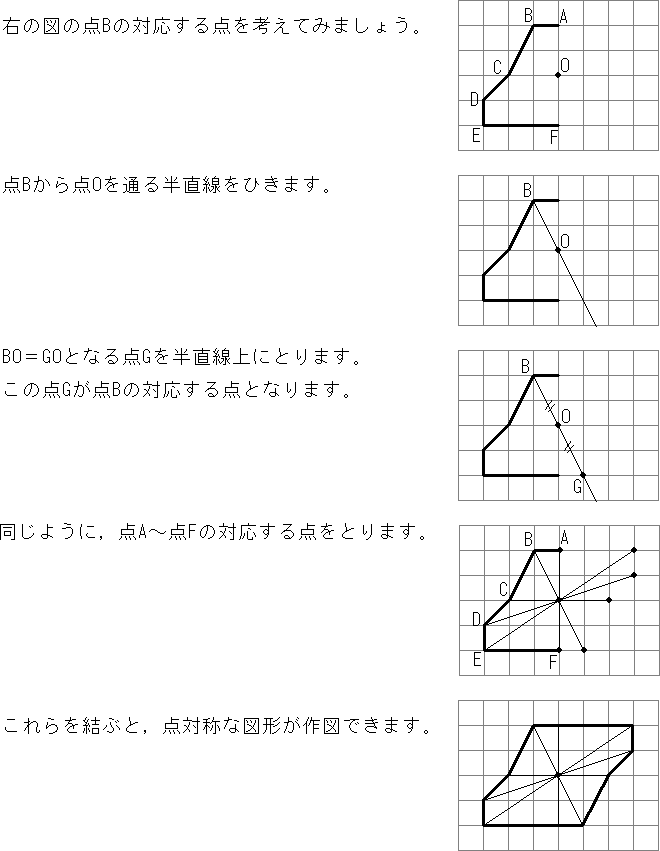
中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン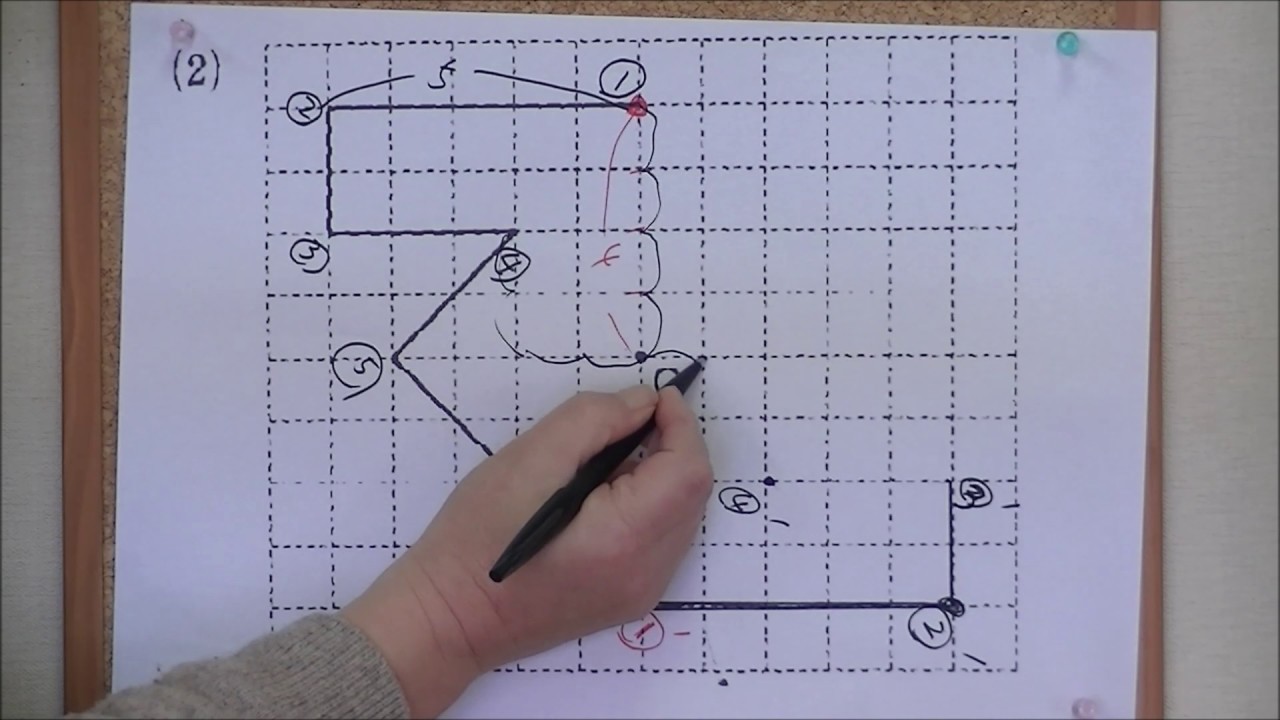
中１数学 点対称な図形とは まなビタミン	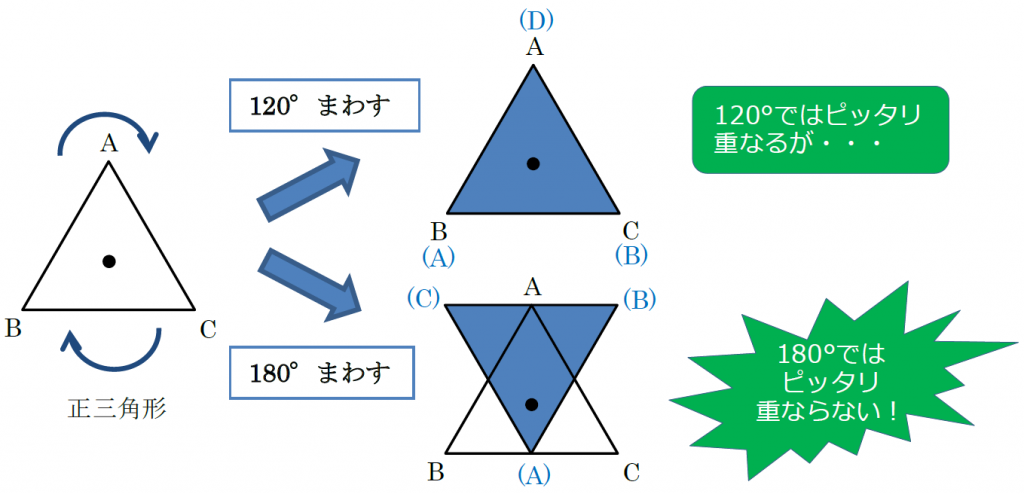中１数学 点対称な図形とは まなビタミン	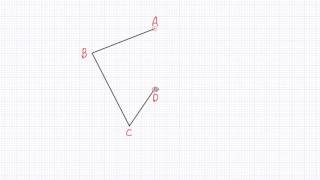中１数学 点対称な図形とは まなビタミン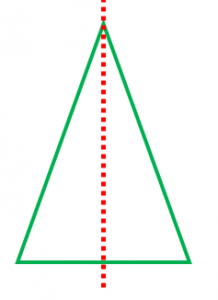
中１数学 点対称な図形とは まなビタミン	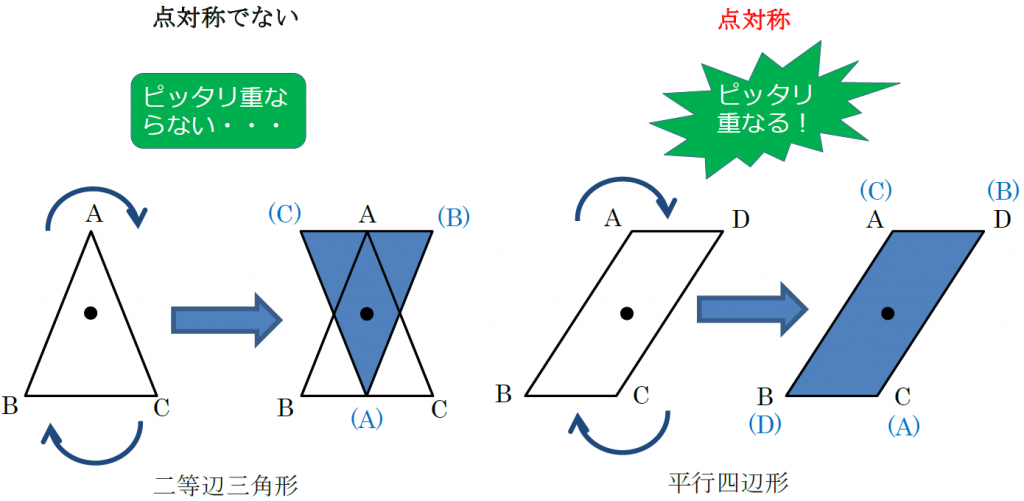中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン
中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン
中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン
中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン
中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン	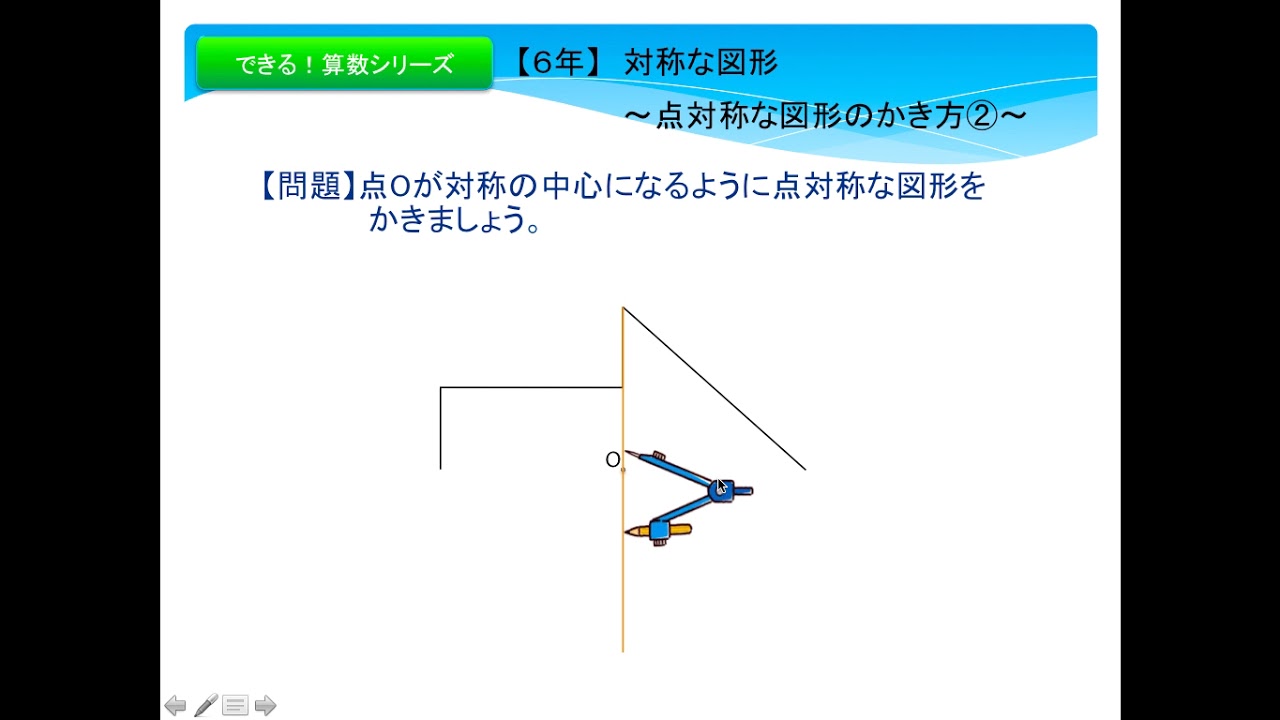中１数学 点対称な図形とは まなビタミン
中１数学 点対称な図形とは まなビタミン	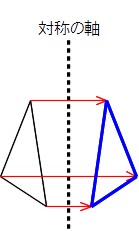中１数学 点対称な図形とは まなビタミン	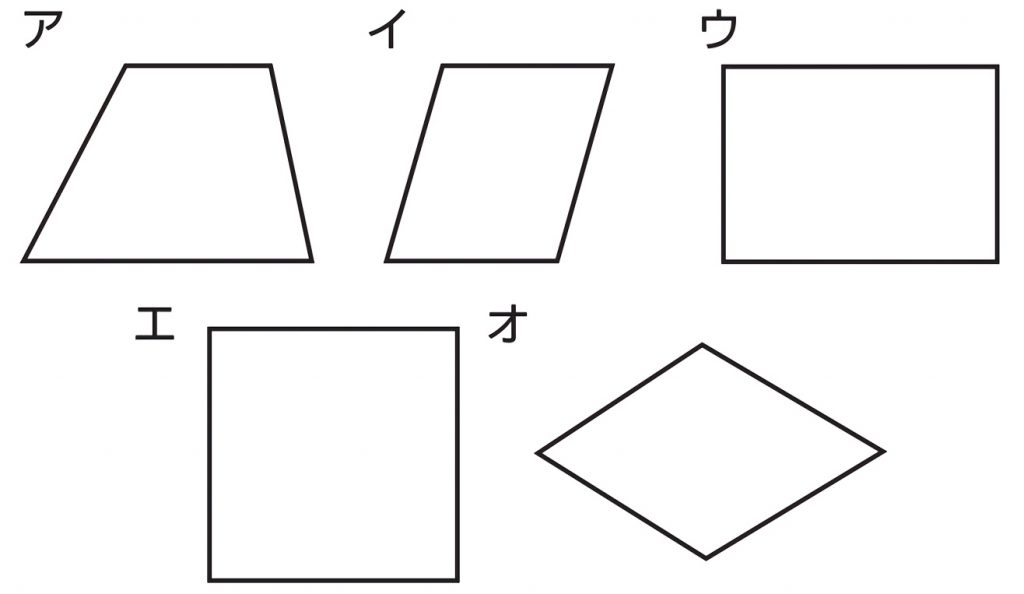中１数学 点対称な図形とは まなビタミン
中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン
中１数学 点対称な図形とは まなビタミン	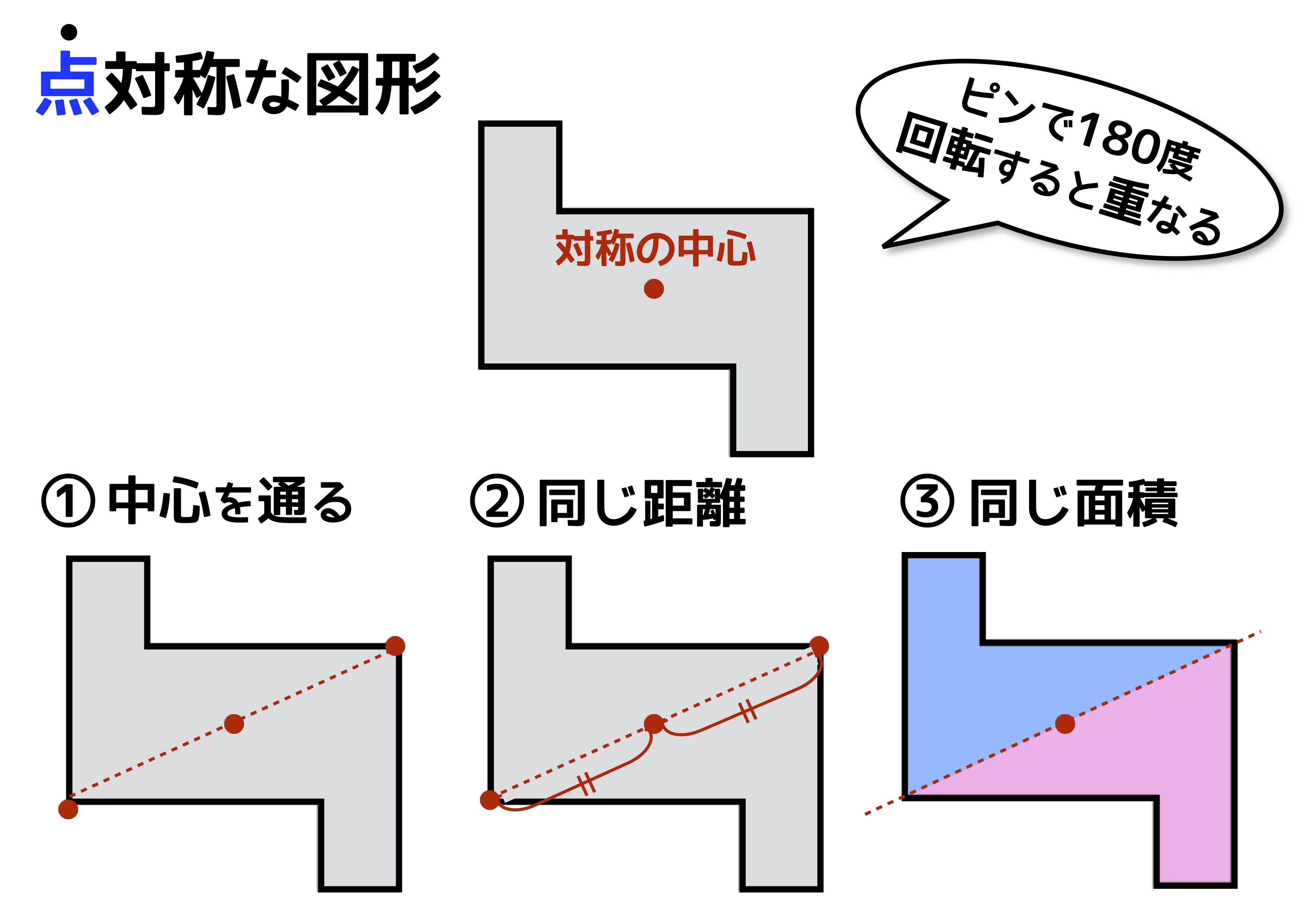中１数学 点対称な図形とは まなビタミン	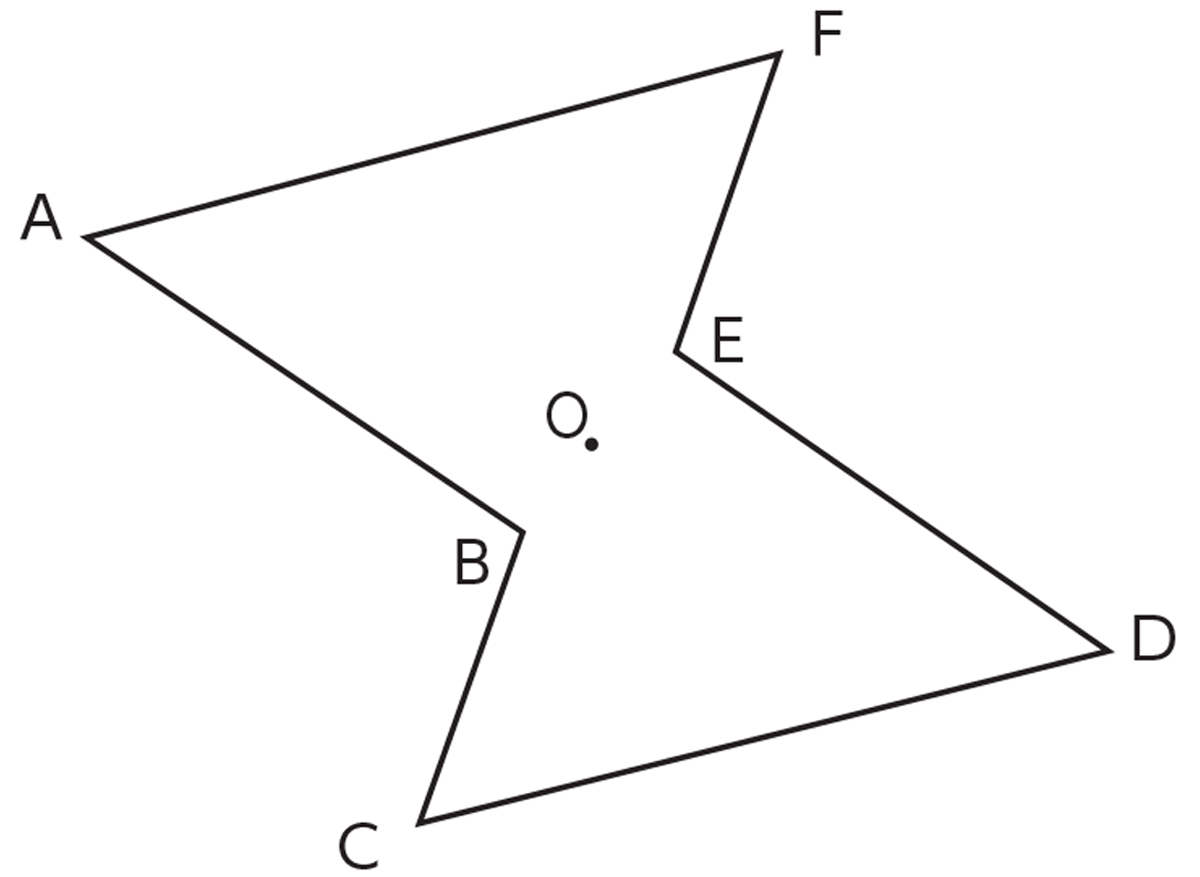中１数学 点対称な図形とは まなビタミン
中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン	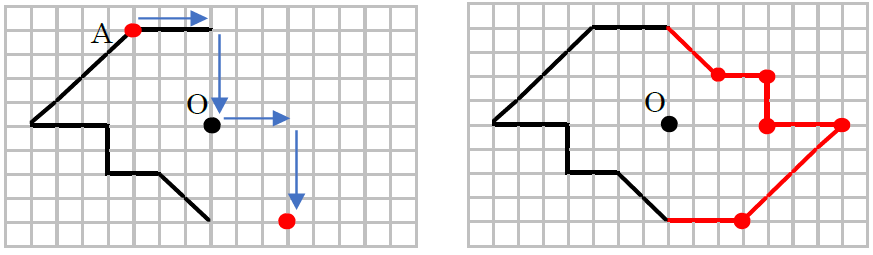中１数学 点対称な図形とは まなビタミン
中１数学 点対称な図形とは まなビタミン	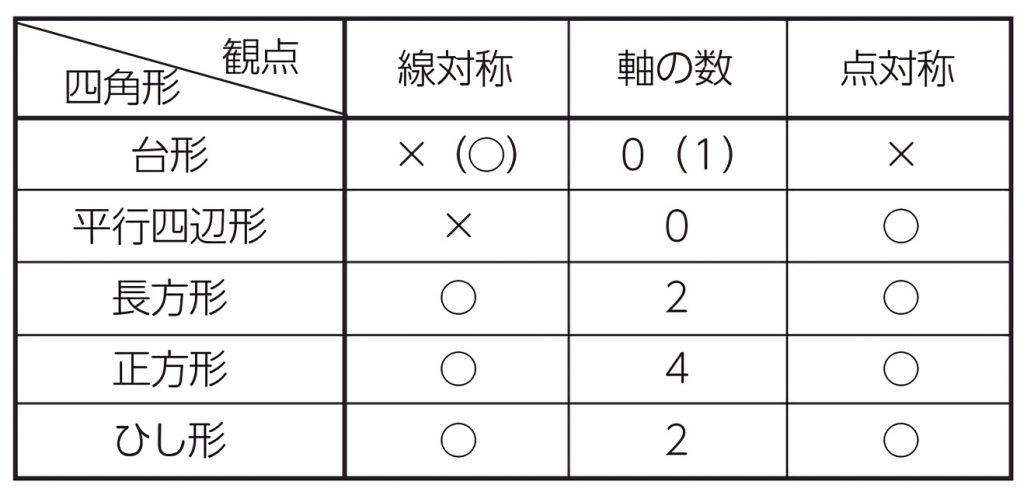中１数学 点対称な図形とは まなビタミン	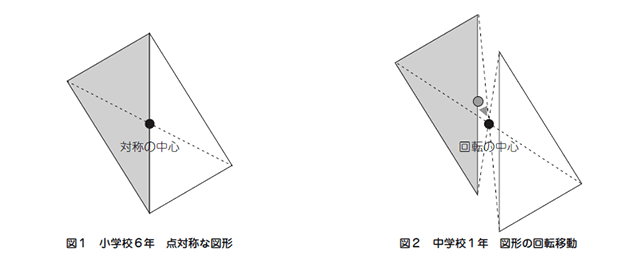中１数学 点対称な図形とは まなビタミン
中１数学 点対称な図形とは まなビタミン	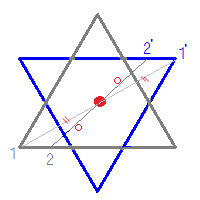中１数学 点対称な図形とは まなビタミン	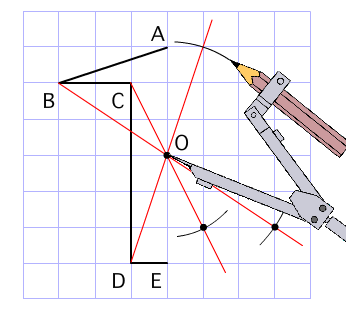中１数学 点対称な図形とは まなビタミン
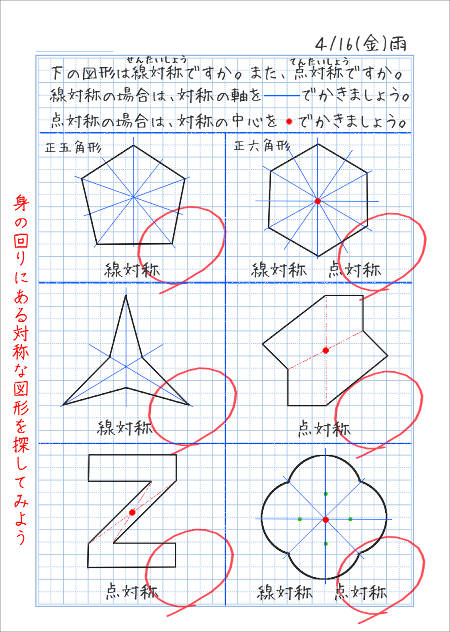中１数学 点対称な図形とは まなビタミン	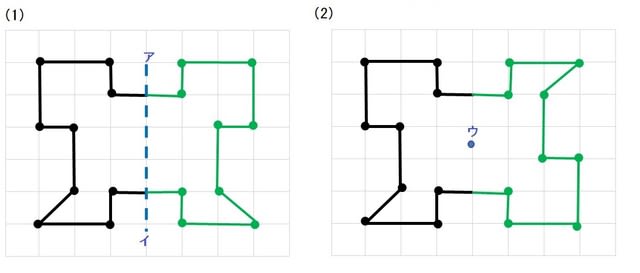中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン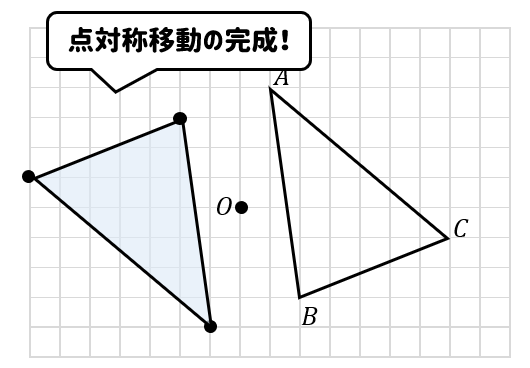
中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン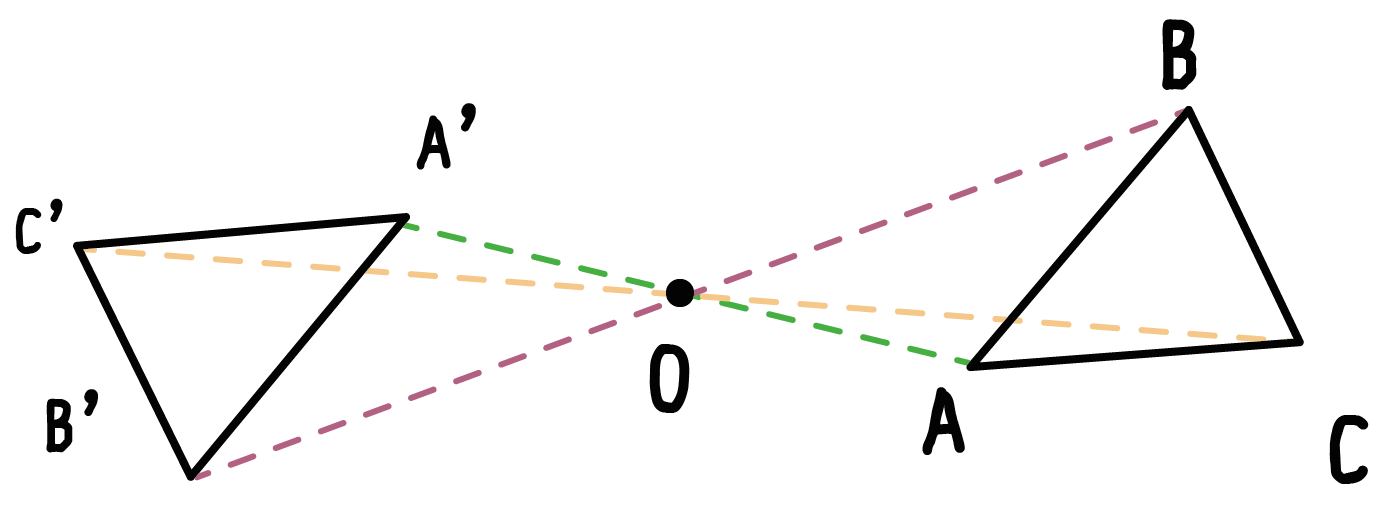
中１数学 点対称な図形とは まなビタミン	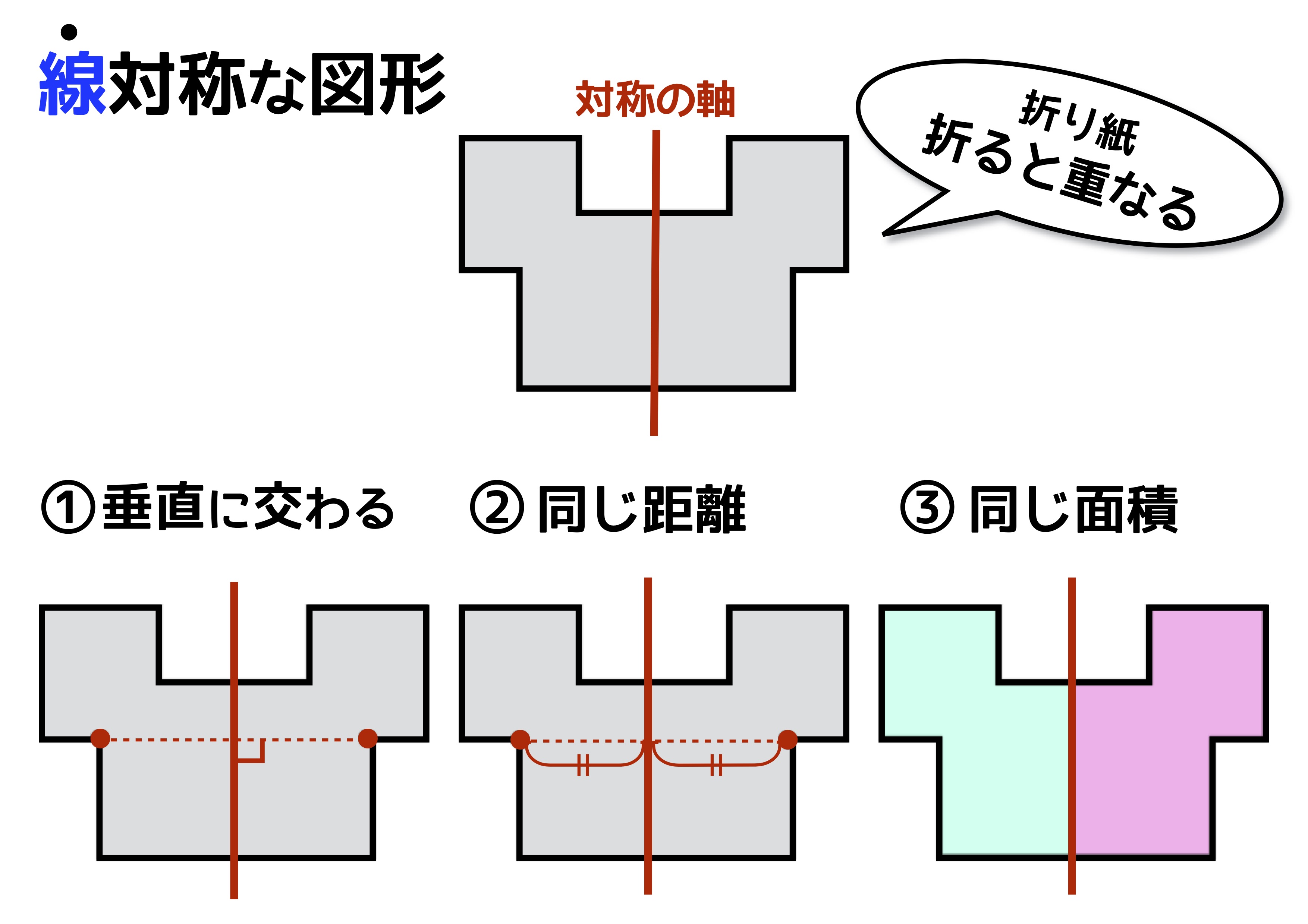中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン
中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン
中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン
中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン
中１数学 点対称な図形とは まなビタミン	中１数学 点対称な図形とは まなビタミン

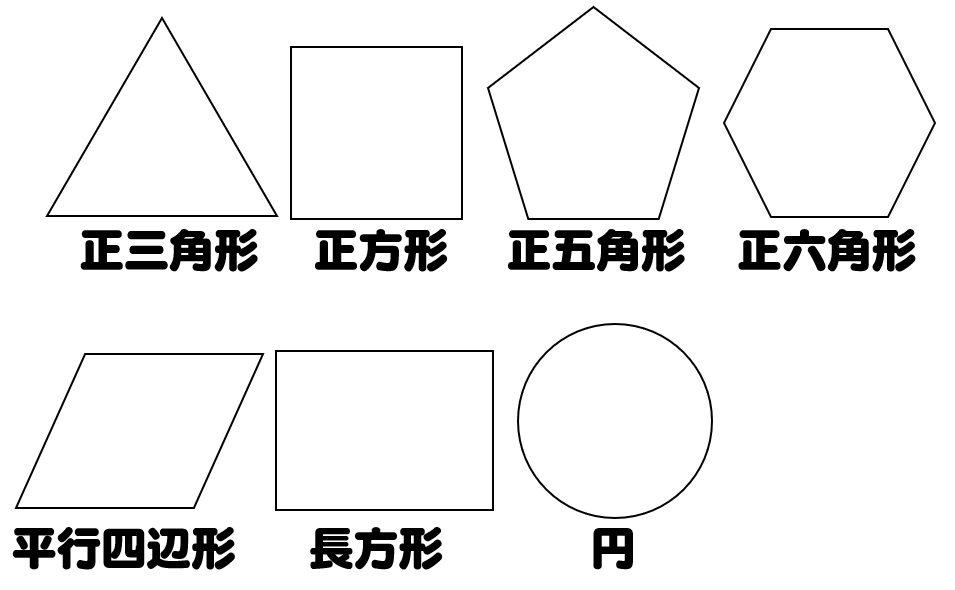
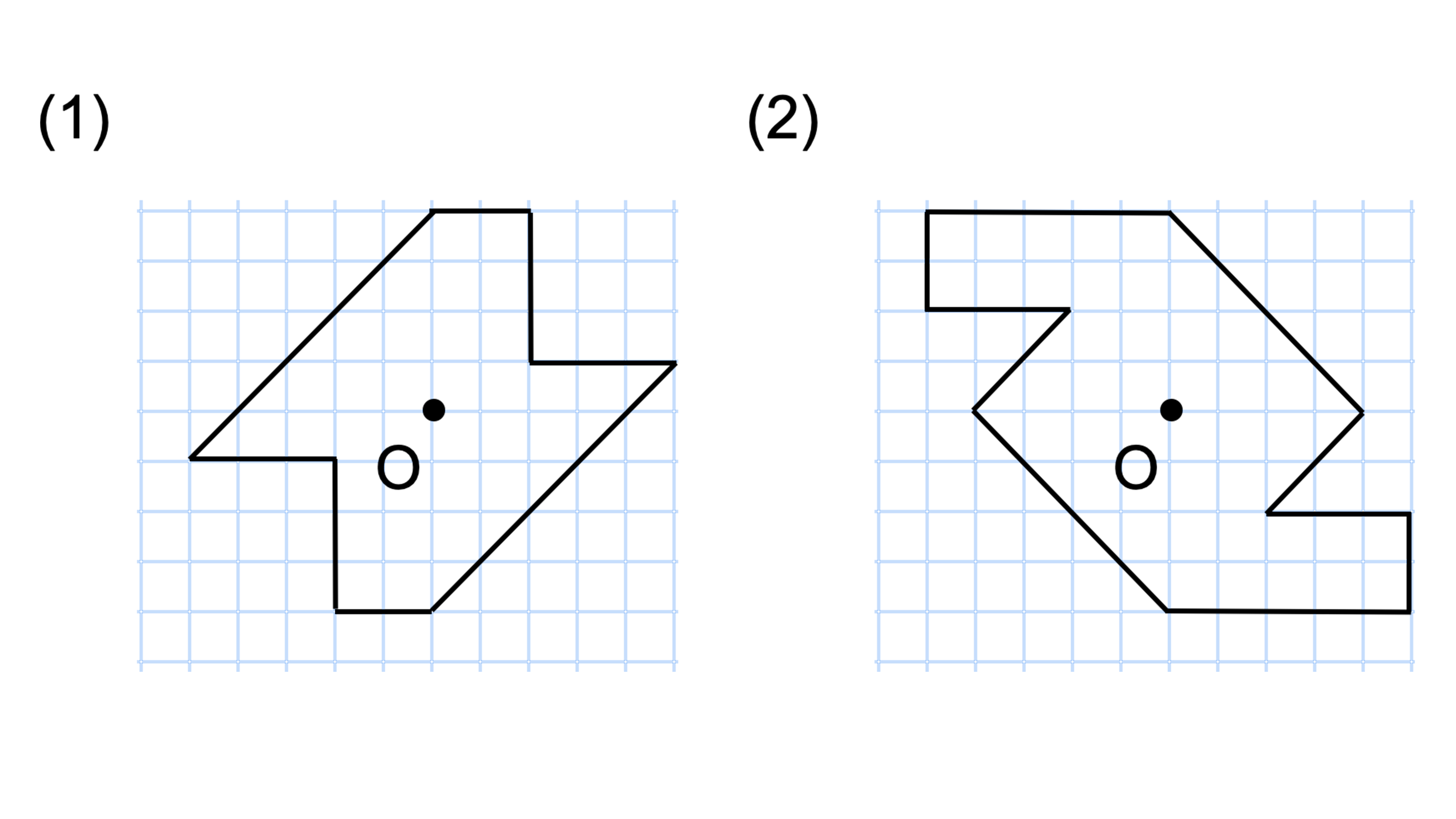
解説 次の図のように，ある点を中心に180°回転させたとき，元の図形と一致する図形を点対称な図形といいます。 このとき回転の中心となる点を対称の中心といいます。 右の図は平行四辺形が対角線の交点を対称の中心とする点対称な図形であることを示しています。 ちょっと点対称の正体がわかったでしょ？？ つぎは点対称移動の書き方をみていこう！ 点対称の図形の書き方ってなにを使えばいいの？？ 点対称移動の作図をマスターするためには、 点対称移動の図形の性質 をおさえておくべきなんだ。

Incoming Term: 点対称な図形の書き方,